 |
|
| 恾怱偲偼廳怱埵抲偺偙偲偱偡丅挿曽宍偺宍側傜懳妏慄偺岎揰偵側傝傑偡丅 抐柺1師儌乕儊儞僩偲椡偺掁傝崌偄岞幃傪棙梡偟偰恾怱傪媮傔傑偟傚偆丅 |
|
|
|
|
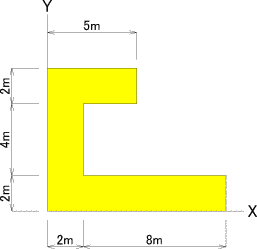
抐柺1師儌乕儊儞僩岞幃偼壓婰偱偡丅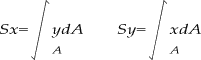 偙傟傪壓婰偺幃乮椡偺掁傝崌偄幃乯偵傾儗儞僕偟偰恾怱傪媮傔傑偡丅 恾怱嫍棧=乮抐柺愊亊恾怱埵抲傑偱偺嫍棧乯偺崌寁亐慡抐柺愊 偱偼丄塃恾偺恾怱傪媮傔偰傒傑偟傚偆丅 |
 |
|
|
|
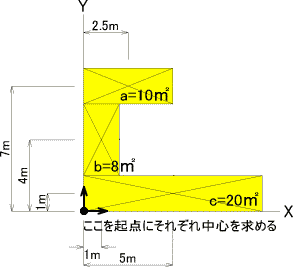
| 恾怱傪媮傔傞偨傔偺壓弨旛傪偟傑偟傚偆 嘆傑偢丄寁嶼偟傗偡偔偡傞偨傔3偮偺挿曽宍偵暘妱偟傑偡丅 嘇暘妱偟偨挿曽宍偺柺愊傪媮傔傑偡丅 丂a亖5m亊2m亖10噓 丂b亖2m亊4m亖8噓 丂c亖10m亊2m亖20噓 嘊X幉丄Y幉偐傜拞怱乮恾怱乯傑偱嫍棧傪媮傔偰偍偒傑偡丅 丂Xa亖7m丂Xb亖4m丂Xc亖1m 丂Ya亖2.5m丂Yb亖1m丂Yc亖5m 偱偼丄寁嶼偟傑偟傚偆丅 |
 |
|
|
|
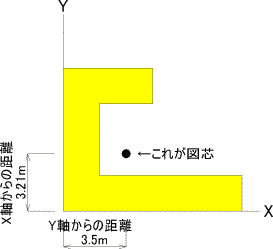
| 恾怱嫍棧=乮抐柺愊亊恾怱埵抲傑偱偺嫍棧乯偺崌寁亐慡抐柺愊 仾傪丄傕偆堦搙巚偄弌偟側偑傜丄X幉曽岦丄Y幉曽岦偦傟偧傟 寁嶼偟傑偡丅 X幉偺寁嶼 Y=乮10亊7亄8亊4亄20亊1乯亐乮20亄8亄10乯 丂=3.21m Y幉偺寁嶼 X=乮10亊2.5亄8亊1亄20亊5乯亐乮20亄8亄10乯 丂=3.5m 摎偊偼丄X幉偐傜3.21m丄Y幉偐傜3.5m偺岎揰偑恾怱偱偡丅 |
 |
|
|
|
| 峔憿寁嶼偱偄偆偲偙傠偺廳怱偼丄寶暔偺廳検傪僾儔僗兛偟傑偡丅 椺偊偽丄2奒偺彴峔柺偱偄偊偽丄1奒偺壆崻晹暘丄忋奒偑偺傞晹暘摍偱偡丅 偦偺條側寁嶼偼丄庤寁嶼偱偼戝曄偱偡偺偱丄崱偱偼傎偲傫偳偑峔憿寁嶼僜僼僩偱寁嶼傪偍偙側偭偰偍傝傑偡丅 |
|
|
|
|
| 姅幃夛幮僇僋婇夋愝寁乵 寶抸抦幆 乶 HOM |
|