
構造計算による住宅設計
長期優良住宅の普及により、
品格法による準耐力壁や床倍率等を用いた計算方法の普及と、
耐震等級という意識が定着してきました。
品格法は任意ですが、
建築基準法施行令第46条(以下令46条)に比べて、より精度の高い耐震チェックが可能となりました。
これらの品格法の耐震等級チェックは、許容応力度計算による構造計算(以下構造計算)をベースに
簡略化して仕様規定されたものです。
構造計算では、品格法による耐震チェックに比べ、さらに詳細な検証をおこないます。
「どうせ、耐震等級2,3を得るのなら、品格法による耐震チェックではなく、
さらに詳細な検証の構造計算をしてもらいたい」
という建築主様も、たくさんいらっしゃるのではないでしょうか。
木造では、あまり馴染みのない構造計算ですが、
ここでは、品格法のベースとなっている構造計算について、
学問的な話ではなくどのようなところが、品格法と、どう違って設計をおこなうのか述べてみたいと思います。
地震力と風圧力の算定と耐力壁の設計
建物に作用する地震力や風圧力を詳細に求めます。
建物重量、建物形状(屋根の形等)、地域、振動特性などを考慮します。
建物が地震に抵抗する、耐力壁の強度をより詳細に求めます。

重心と剛心と平面不整形
平面不整形のパターン
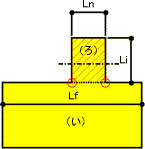 |
| (a)突出部を有する平面形 |
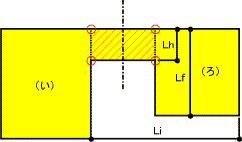 |
| (b)くびれを有する平面形 |
令46条の計算では、考慮されない(品格法では考慮される)準耐力壁量を加算すると、同じ耐力壁量であるにもかかわらず、数値が増しますので安全側になってしまい、逆に不安になられる方もいらっしゃるかと思いますが、建物全体に与える影響を、詳細に検証するには、大変有効です。
例えば、重心と剛心のズレ(偏心率)をより正確に求めることができます。
重心とは、建物の重さの中心です。家相でいえば極みたいなものです。
地震力は、その階の重心に作用しようとします。
それに対して、剛心は、耐力壁の強さの中心です。
重心と剛心のズレが大きいと、地震時に建物がねじれて剛性の低下を招きます。
重心と剛心のズレを偏心率というのですが、0.3以下におさえなければいけません。
また、設計において右図のように突出部やくびれ等を有するいわゆる平面不整形は、構造計画上なるべく避けたほう良いです。
これは、右図でいうと、地震時に(い)のゾーンと(ろ)のゾーンが逆位相で揺れたり、片方のゾーンが大きく偏心して回転しながら揺れたりして赤斜線部分が破損する可能性が高いからです。
ですが、なかなか敷地の条件によりどうしても採用せざる得ない場合もあります。
「木造軸組工法住宅の許容応力度設計」の4.7.1平面不整形建築物の構造安全性の検討では、
図の一点鎖線部分で、建物を(い)(ろ)のゾーン分けをし、それぞれのゾーン毎で「荷重」「外力」「鉛直構面の剛性」などを算定し、最後に地震力に対する検定比小さい方の値/大きい方の値≧3/4を確認することとなっています。
|
|

筋違いの方向性
一般の計算でおこなう筋違い計算、すなわち、品格法や令46条の計算では、筋違いには方向性がないものと仮定されています。
例えば、品格法や令46条の筋違い計算では、45×90の筋違いの壁倍率は2倍ですが、
方向性を考慮しないため、現実の壁耐力とは違った値が発生する場合があります。
ちょっと極端な例ですが、下記に例を示します。
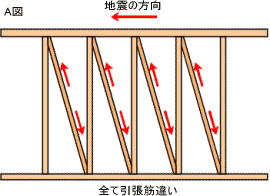 |
左A図の条件
地震方向:左向き
柱間隔:0.91m
筋違い:45×90
計算式:壁倍率×壁長さ(m)=壁の強さ
品格法や令46条の計算では、
2(倍)×0.91(柱間隔)×4(ヶ所)=7.28(壁の強さ)
でも、構造計算では、
1.5(倍)×0.91(柱間隔)×4(ヶ所)=5.46(壁の強さ)
|
7.28-5.46=1.82と、25%も壁の強さを多く、見積もってしまいます。
品格法の計算上、間違いではありませんので、
例え品格法による住宅性能表示制度を利用した住宅や、長期優良住宅の設計審査も、
お役所の決済は受けられるのですが。
でも、多分、こんな極端な例だと、これまずんじゃね?とはいわれそうですが
この様に、実際は、筋違いには方向性があり、構造計算では、上記の場合、引張筋違いは1.5倍、圧縮筋違いは2.5倍と方向性を考慮します。
どうして、品格法による筋違い計算では、筋違いの方向性を考慮してないかと言いますと、
第一に、計算の簡略化、
第二に、筋違いは交互に入れると仮定されているからです。
(交互に入れるので引張筋違い1.5倍と圧縮筋違い2.5倍の平均値として簡略値の2倍を採用している)
ということは、交互に筋違いを入れないと品格法や令46条の筋違い計算の仮定が崩れることを意味します。
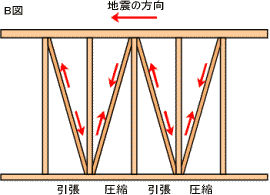 |
実際、左B図のように交互に入れた場合は、
同じ計算結果となります。
条件はA図と同じ。
品格法や令46条の計算では、
2(倍)×0.91(柱間隔)×4(ヶ所)=7.28(壁の強さ)
構造計算では、
1.5(倍)×0.91(柱間隔)×2(ヶ所)+2.5(倍)×0.91(柱間隔)×2(ヶ所)=7.28(壁の強さ)
|
もし、お宅の建物が、バランス良く筋違いを入れてくれてない場合は、「交互に入れてよ」と注意して下さい。
※構造計算による筋違い計算は、実際はもう少し複雑ですが、説明のため大雑把にしております。
|
|
▲TOP
床倍率の設計(水平構面の構造計算を省略できる条件)
耐力壁が、壁倍率を用いて計算するように、
床も、地震力や風圧力に耐えられるか、床倍率により計算します。
※構造計算では、床倍率とは言わず、単位長さあたりの許容せん断耐力ΔQa(kN/m)
品格法による床倍率計算と基本的には同じですが、
構造計算の場合は、床倍率計算は水平構面の構造計算を省略できる条件という位置付けです。
床倍率計算により、クリアしない場合(NGの場合)は、
床せん断耐力による検証(より詳細な検証)をしなければなりません。
逆に言えば、品格法による床倍率計算でクリアしなくても、構造計算により、クリアする可能性があると言うことです。

水平構面の役割 について
水平構面とは、水平力に抵抗する構造躯体で「屋根」「床」「火打ち」で構成されています。
地震や台風などの水平力に抵抗するには、その水平構面を固めて建物全体が一体となる必要があります。
耐力壁の前提条件で、重要な要素です。
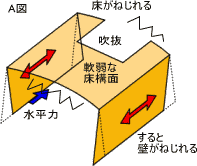 |
水平構面が弱いと、どんなに耐力壁をバランス良く設けても、
A図のように耐力壁の変形量が大きくなり、
本来の力を発揮しません。
|
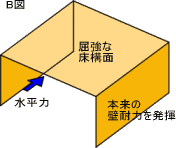 |
それに対し、B図のような充分な強度を持った水平構面であれば、
水平力を受けた時に、その水平構面が一体となって抵抗し
その下にある、耐力壁の変形量も少なくすみ、
本来の耐力壁の強さを発揮します。
|
この項目は、建物の構造耐力に、もの凄く、大変重要な要素ですが、一般にはあまり馴染みが無いためか、意識からすっぽりと抜け落ちております。
構造計算をおこなわない場合でも最低限チェックしたい項目です。
|
|
▲TOP
柱頭柱脚の接合部の設計
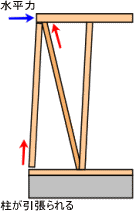 |
耐力壁の柱には地震や台風などの水平力が生じた場合、
筋違いが、抵抗し上方向へ柱を突き上げようとする力が発生します。
それが、柱の引抜き力です。
考え方の概念として、
壁耐力が大きい所に、大きな引抜き力が発生します。
例えば、建物の隅とか、ダブルで筋違いを入れたところとかです。
|
筋違いには、圧縮側と引張側という方向性がありますので、
補正値である係数という値を加えて計算をおこないます。
※同じ耐力に挟まれた柱には引抜き力は原則発生しません。
で、柱の仕口のほぞ差し等は、横方向のズレには抵抗しますが、引抜き力には無力なので、接合金物の耐力により、引抜き力に抵抗するのですが、
その接合金物が引抜き力に耐えられるかどうかの検証をします。
構造計算による柱頭柱脚の接合部の計算には
「N値法」「ラーメン置換法」「せん断法」などがありますが、
品格法によるN値計算と、大きく違うところは、
荷重分布図(オリジナルメモPDF)により算出した押え効果(カウンターウェイト)加味して、さらに、回転力を詳細に求めた計算をおこなうところです。
▲TOP
横架材の接合部の設計
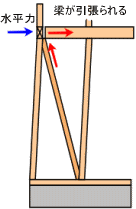 |
横架材とは梁のことですが、
その梁は、地震などの水平力が作用すると、
筋違いの押し上げる力により、引抜き力が発生し、
外れようとします。
|
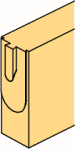
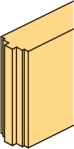
大入れ蟻掛け
(梁対梁) |
ほぞ差し
(梁対柱) |
プレカットによる継手仕口はおおまかに分けて
左図の2種類が主に使われますが、
この仕口は引抜き力に対しては無力です。
それらを接合金物の耐力によりカバーしているわけですが、
大きな地震がきても、外れない、又は仕口が外れても、
金物のせん断耐力により落下倒壊しないかを検証します。
|
 |
 |
品格法では、計算ではなく、仕様規定によりチェックします。
 損傷しても倒壊しなければOKと判断 損傷しても倒壊しなければOKと判断
え?と思われるかもしれませんが、構造計算の概念として、
損傷しても倒壊しなければOKと判断する場合もあります。
過去の地震被害から、木造軸組は損傷しても改修すれば、比較的元に戻りやすいこともあります。
たとえば、品格法による耐震等級2は、
「数百年に一度発生する地震の1.25倍の地震力に対して倒壊・崩壊せず、数十年に一度発生する地震の1.25倍の地震力に対して損傷しない程度」
と定められています。
大変悩ましい問題ですが、どこまでの耐震性を求めるかは、
コストとの兼ね合いがあります。
極端な話、完璧な耐震性の建物などこの世には存在しません。
あるとすれば、原子力発電所や核シェルターでしょうが、
そこまでコストをかけると、とんでもない金額になるでしょうから、誰も家を買えませんよね。
|
|
▲TOP
土台の曲げと接合部の設計
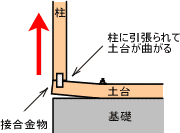 |
柱脚に引抜き力が発生した場合(地震等の短期荷重)、
その接合金物の耐力により、土台と基礎が離れる引張り力が働きます。
土台が曲がる力に十分抵抗できるかの検証をおこないます。
また、耐力壁の作用により、土台が基礎上を横方向にずらそうとします。それらの引抜き力やせん断力に耐えられるかのアンカーボルトの検証です。
|
品格法のチェック項目に含まれておりません。
▲TOP
構造計算で言うところの鉛直荷重に対しては、一般的な柱寸法105角で充分な場合がほとんどです。
割り箸など、細いものでも、垂直方向に押えても結構頑丈ですよね。
が、細長いが故に横方向の荷重には弱いのが柱です。
一見、柱には上からの荷重(鉛直荷重)のみで、水平方向の荷重など関係なさそうですが、
実は、かなりあります。
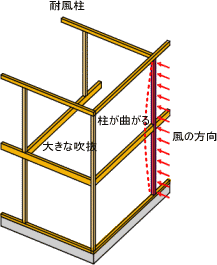
| 耐風柱 |
耐風梁 |
|
 |
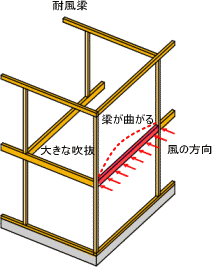 |
その代表的なものは、風です。
何かと、地震ばかりが注目されてる構造ですが、
台風もかなりやばい力が住宅に働きます。
構造計算では、大きな吹抜をつくる場合や、台風などの風圧力によって、その影響を受けるヶ所には、
その柱又は梁がボキっと折れたりしないか、十分検討をおこないます。
|
品格法のチェック項目に含まれておりません。
▲TOP
小屋梁・床梁・母屋・垂木・根太の設計
梁等の検証において重要なのは、
荷重の算定と、梁がその荷重をどのように分配して負担するかの荷重負担面積が重要な要素だと思います。
長期と短期に分けてそれぞれ検証をおこなうのですが、
長期に関しては、荷重の算定が重要な要素です。
建築構造ポケットブックに積載荷重の一般的な数値が載ってますので、
それに基づいて基本計算をおこなうのですが、
部分的に荷重負担が増しそうなヶ所は別途検証をしたいものです。
ユニットバスはこちらでもすぐにわかるのですが、
グランドピアノ、ウォーターベットなど特別に重い物は、教えて頂かないといけません。
品格法のチェック項目に含まれておりません。

意外と重い本棚
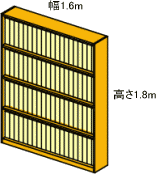 |
例えば、幅1.6m高さ1.8mの本棚にギュウギュウ詰めに本を入れた場合、
条件
紙の重さ:約128g/㎡
紙の厚さ:約0.1㎜→メータに換算0.0001m
本1頁の面積:0.3m(高さ)×0.21m(奥行)=0.063㎡
計算
1.6(棚幅)/0.0001(紙厚)=16000(1.6m当り枚数)
0.21(本幅)×0.3(本高)×16000(1.6m当り枚数)=1008(1段㎡)
1008(1段㎡)×4(段)=4032(総㎡)
4032(総㎡)×128(g)=516096g→キロに換算516kg
ということで、500㎏を超えます。
|
これは、一般的なグランドピアノ約400㎏に匹敵又は超える荷重です。
せっかく構造計算をおこなうのなら、こんな所にも注意したいものです。
|
|
▲TOP
基礎の設計
軸組の構造がいくらしっかりしても、それを支える基礎が弱かったらどうにもなりません。
さらに、基礎がいくらしっかりしてもそれを支える地盤がふにゃふにゃならどうにもなりません。
したがって、基礎の設計では、初めに、地盤の強度を知る必要があります。
調査方法ですが、木造3階建て程度なら、スウェーデンサウンディング試験が一般的な方法です。
地盤が強いかどうかを判断するには、地盤の許容応力度と沈下量が重要な要素ですが、木造の場合は建物荷重は軽いですから、
地盤の許容応力度より先に、沈下量がNGになる場合がほとんどです。
「建築基礎構造設計指針」では、沈下量は10㎝以下と定められていますが、
瑕疵保証の基準は5㎝以下がほとんどだと思いますが、
地盤改良等は高い確率で必要になると覚悟した方がよろしいかと思います。
基礎に関しては、地盤調査の地盤の許容応力度にもとづき、下記のようなことをおこないます。
品格法では計算ではなく、スパン表など仕様規定が設けられてます。
▲TOP
ご意見投稿
左欄のお問い合せメニューもご利用下さい。
|
|